DEAR INVESTOR JUAN
Dear Investor Juan,
I just got a loan for 450k 36months to pay.. I see a per annum rate of 28.58% but she was saying something about 1.29% per month add on rate.. Im confused, mind explaining it to me the add on rate?
Thanks,
Mon
Dear Mon,
I have already discussed the difference between add-on rate and the monthly compounded interest rate (such as in credit card debt or home and car loans) in this post, but I will try to explain in again and apply it to your situation.
With add-on interest, the quoted monthly add-on interest rate is multiplied to the principal or loan amount to get the monthly interest payment. For the monthly principal repayment, the loan amount is divided by the loan duration. In your case, therefore, the monthly interest payment is 1.29%*450,000 = 5,805, while the monthly principal repayment is 450,000/36 = 12,500, and the total monthly payment is 5,805 + 12,500 = 18,305, an amount that you would have to pay every month, as seen in the spreadsheet below. If you scroll down to the bottom of the sheet, you'll see that at the end of 36 months, you will have paid a total of 658,980, of which 208,980 is for interest. Further down, you'll see that the internal rate of return or IRR, a way to compute for return or interest while considering the timing of payments, is 26.72%. This is not exactly what your bank representative quoted, but this may be what she was talking about.
Now if we were to take the same monthly interest rate of 1.29% but this time apply it as a monthly compounded rate in an amortized loan, then we'll see a different payment schedule. Please refer to the spreadsheet below.
To get the monthly payment (or "amortization") of this kind of loan, we have to use the PMT function of Excel or any spreadsheet program, where "rate" = 1.29%, "nper" = 36, and PV = -450,000. The resulting figure is 15,705, which is the amount that is paid every month until the 36th month. In the first payment, 1.29%*450,000 = 5,805 goes to interest, same as in the add-on loan, so 15,705 - 5,805 = 9,900 goes to principal. The following month, the principal goes down to 450,000 - 9,900 = 440,100, which will then become the basis for this month's interest payment of 440,100*1.29% = 5,677. Do you now see how this kind of loan is different from your add-on loan?
With monthly compounded interest loans, principal repayments are deducted from the principal, the lower principal balance becomes the basis for interest computation, and interest payments decline (and in the case of amortized loans where the monthly payment is constant, principal payments increase) as the end of the loan period nears. With add-on interest, monthly interest payments stay the same even as part of the principal is repaid every month. And this is why, at the same "monthly interest rate," add-on interest loans are more expensive than monthly compounded debt.
I hope I was able to explain the add-on rate sufficiently, Mon. Good luck.
Thursday, May 30, 2013
Monday, May 27, 2013
Concerns about Early Retirement
DEAR INVESTOR JUAN
Dear Investor Juan,
I've been reading your blog and I find it entertaining and at the same time educational. I have a few questions for you but let me give you a little background about myself. I am 27 years old and single. Been working as a caregiver and my goal is to quit work by next year and follow my long time dream of becoming a lay missionary. I wasn't able to follow my dream coz my family needed me financially and now that I settled them already, it's time for me to follow my heart's desire.
Let me give you and idea on my financial life and please tell me if you think I can follow my goal or if I should extend a year or two before quitting work for good.
Net worth: Php 4 Million
Mutual fund : Php 150k
Stocks: Php 1M
Debt : 0
Other investments : Small land
Home: owned
I am a frugal person and live simply. I am also a minimalist and I don't dabble in consumerism. I'm planning on not touching my paper assets till I'm old. I also have emergency fund worth 6 months of living expenses. However, I don't have insurance and would like to avail one. Please take note that I'm single and with no beneficiary.
You think it's possible to quit work and "forget" about my paper assets and just move on with life without adding to it? How much you think my money would grow in 40 years considering inflation? I'm still investing 70-80 percent of my income as of the moment. How am I doing financially. I am a voluntary celibate and don't plan on marrying in the future so please consider that too esp with health care cost with no one to share the expenses when I'm old.
Sorry if I have tons of questions. I just needed some advice on where I stand financially or if I can quit work by next year coz I feel so empty. I keep thinking if next year is the time where I can say to myself that " My earning days are over. Time for me to follow my dream"
Good luck and thanks so much,
Cory
(Additional information in response to a follow-up email.)
4 million consist of emergency fund, mutual fund, stocks and the townhouse in Cebu (subdivision) which actually appraised at 1.3M and its in use (that's where I will live once I get home). My other land is totally small and idle that I did not count it in my asset. I consider my townhouse an asset, though.
My expected expenses is P15k (scrimp) - P25k (splurge). I'm totally used to simple life and would like to live frugally. I am planning to live on my townhouse that I own when I grow old which is situated in Mactan, Cebu or I'll probably move somewhere quiet depending on the cost of living as long as its safe. I'm not maarte :) (Emphasis is mine. - IJ)
Thanks a bunch.
Cory
Dear Cory,
Choosing to retire early compounds the "retirement problem" because the longer retirement period increases funding requirement, and at the same time, the smaller earning window makes it harder to meet the higher retirement fund target. It's still possible, though, if one starts saving early enough and earns (and saves) high enough. And from the information you've provided, I think you meet both criteria to a certain degree, we just have to see if you meet the criteria well enough.
It's time to crunch some numbers (since we can't really use the 30-60-90 framework that I introduced a couple of posts back).
Let's start by assuming that your assets will earn just enough returns to be able to beat inflation so that the spending power of your assets is constant throughout the planning horizon. Speaking of planning horizons, the typical end-of-horizon age planners use is 90 years, so let's start with that.
Retirement period = 90 - 28 = 62 years * 12 = 744 months.
Net worth = 4,000,000/744 months = 5,376 pesos per month. Can you live on this amount?
Honestly, 90 years may be a bit conservative since it's well above the estimated life expectancy of Filipinos (or people living in the Philippines?) of around 68 years. If we use 80 years, we get:
Retirement period = 80 - 28 = 52 years * 12 = 624 months.
Net worth = 4,000,000/624 months = 6,410 pesos per month. Better, but maybe still not enough.
Things don't look so good given the above assumptions. But if you subscribe to the concept of long-term passive investing, something like Jeremy Siegel's "stocks for the long run" argument (to which I completely adhere, but that's for another post), then the returns on your assets should be able to reliably beat inflation year-on-year and give your assets more spending power. The question is: how much more?
Please consider the timeline at the top of the image above. Say you withdraw an amount X from your assets for your expenses on your first year of retirement. The following year, you withdraw a higher amount, X*(1+g), where g is the average annual inflation rate. You keep on doing this until age 89, where you withdraw an amount equal to X*(1+g)^61.
The sum of your withdrawals should of course be less than or equal to your total net worth of 4 million plus your investment returns, if your assets earn annual average return of i. Then, what would be the largest value of X given that you have 4 million in assets today, your assets can earn an annual return of i, and annual inflation is g? There are several approaches in solving for X, but the most straightforward is to get the present value of the withdrawals and equate it to 4 million using the formula:
The average annual inflation rate in the Philippines in the past 10 years is around 4.5% (I thought it would be lower for outside the NCR, but it's not. This figure is for the entire country), so let's use that for g. Let's assume that you'll invest your assets in a diversified portfolio of stocks such that you'll earn the average annual return of the PSEi. I don't have exact numbers at the moment, so let's just use i = 7%, which I believe is a conservative estimate (given that the S&P 500 has had an annualized return of close to 10% in the past 25 years). Solving for X as shown in the image above, we get:
@ g = 4.5%, i = 7%, X = 122,394 or 10,200 per month. More workable?
Of course, higher assumptions for i would further improve the situation.
@ g = 4.5%, i = 8%, X = 149,695 or 12,475 per month
@ g = 4.5%, i = 9%, X = 178,797 or 14,900 per month
You'll notice that this last estimate almost meets your "scrimp" budget, so I think your plan is workable. To make it really work, though, you would have to keep most of your assets in equities so that you'll have a higher chance of beating inflation every year, and beating it by a higher amount. Also, I still strongly encourage you to stick to the DRREW plan--particularly, always have some amount ready for unexpected expenses and get some form of private health insurance.
Finally, you may want to delay retirement for a few years and maybe build up your funds to 5 or 6 million. Try to play with the equation, change 4 million to a higher amount and instead of 60 change the exponent to years of retirement - 1, and see by how much X will increase.
Dear Investor Juan,
I've been reading your blog and I find it entertaining and at the same time educational. I have a few questions for you but let me give you a little background about myself. I am 27 years old and single. Been working as a caregiver and my goal is to quit work by next year and follow my long time dream of becoming a lay missionary. I wasn't able to follow my dream coz my family needed me financially and now that I settled them already, it's time for me to follow my heart's desire.
Let me give you and idea on my financial life and please tell me if you think I can follow my goal or if I should extend a year or two before quitting work for good.
Net worth: Php 4 Million
Mutual fund : Php 150k
Stocks: Php 1M
Debt : 0
Other investments : Small land
Home: owned
I am a frugal person and live simply. I am also a minimalist and I don't dabble in consumerism. I'm planning on not touching my paper assets till I'm old. I also have emergency fund worth 6 months of living expenses. However, I don't have insurance and would like to avail one. Please take note that I'm single and with no beneficiary.
You think it's possible to quit work and "forget" about my paper assets and just move on with life without adding to it? How much you think my money would grow in 40 years considering inflation? I'm still investing 70-80 percent of my income as of the moment. How am I doing financially. I am a voluntary celibate and don't plan on marrying in the future so please consider that too esp with health care cost with no one to share the expenses when I'm old.
Sorry if I have tons of questions. I just needed some advice on where I stand financially or if I can quit work by next year coz I feel so empty. I keep thinking if next year is the time where I can say to myself that " My earning days are over. Time for me to follow my dream"
Good luck and thanks so much,
Cory
(Additional information in response to a follow-up email.)
4 million consist of emergency fund, mutual fund, stocks and the townhouse in Cebu (subdivision) which actually appraised at 1.3M and its in use (that's where I will live once I get home). My other land is totally small and idle that I did not count it in my asset. I consider my townhouse an asset, though.
My expected expenses is P15k (scrimp) - P25k (splurge). I'm totally used to simple life and would like to live frugally. I am planning to live on my townhouse that I own when I grow old which is situated in Mactan, Cebu or I'll probably move somewhere quiet depending on the cost of living as long as its safe. I'm not maarte :) (Emphasis is mine. - IJ)
Thanks a bunch.
Cory
Dear Cory,
Choosing to retire early compounds the "retirement problem" because the longer retirement period increases funding requirement, and at the same time, the smaller earning window makes it harder to meet the higher retirement fund target. It's still possible, though, if one starts saving early enough and earns (and saves) high enough. And from the information you've provided, I think you meet both criteria to a certain degree, we just have to see if you meet the criteria well enough.
It's time to crunch some numbers (since we can't really use the 30-60-90 framework that I introduced a couple of posts back).
Let's start by assuming that your assets will earn just enough returns to be able to beat inflation so that the spending power of your assets is constant throughout the planning horizon. Speaking of planning horizons, the typical end-of-horizon age planners use is 90 years, so let's start with that.
Retirement period = 90 - 28 = 62 years * 12 = 744 months.
Net worth = 4,000,000/744 months = 5,376 pesos per month. Can you live on this amount?
Honestly, 90 years may be a bit conservative since it's well above the estimated life expectancy of Filipinos (or people living in the Philippines?) of around 68 years. If we use 80 years, we get:
Retirement period = 80 - 28 = 52 years * 12 = 624 months.
Net worth = 4,000,000/624 months = 6,410 pesos per month. Better, but maybe still not enough.
Things don't look so good given the above assumptions. But if you subscribe to the concept of long-term passive investing, something like Jeremy Siegel's "stocks for the long run" argument (to which I completely adhere, but that's for another post), then the returns on your assets should be able to reliably beat inflation year-on-year and give your assets more spending power. The question is: how much more?
 |
| Click to enlarge |
Please consider the timeline at the top of the image above. Say you withdraw an amount X from your assets for your expenses on your first year of retirement. The following year, you withdraw a higher amount, X*(1+g), where g is the average annual inflation rate. You keep on doing this until age 89, where you withdraw an amount equal to X*(1+g)^61.
The sum of your withdrawals should of course be less than or equal to your total net worth of 4 million plus your investment returns, if your assets earn annual average return of i. Then, what would be the largest value of X given that you have 4 million in assets today, your assets can earn an annual return of i, and annual inflation is g? There are several approaches in solving for X, but the most straightforward is to get the present value of the withdrawals and equate it to 4 million using the formula:
The final equation is boxed in the image above.
The average annual inflation rate in the Philippines in the past 10 years is around 4.5% (I thought it would be lower for outside the NCR, but it's not. This figure is for the entire country), so let's use that for g. Let's assume that you'll invest your assets in a diversified portfolio of stocks such that you'll earn the average annual return of the PSEi. I don't have exact numbers at the moment, so let's just use i = 7%, which I believe is a conservative estimate (given that the S&P 500 has had an annualized return of close to 10% in the past 25 years). Solving for X as shown in the image above, we get:
@ g = 4.5%, i = 7%, X = 122,394 or 10,200 per month. More workable?
Of course, higher assumptions for i would further improve the situation.
@ g = 4.5%, i = 8%, X = 149,695 or 12,475 per month
@ g = 4.5%, i = 9%, X = 178,797 or 14,900 per month
You'll notice that this last estimate almost meets your "scrimp" budget, so I think your plan is workable. To make it really work, though, you would have to keep most of your assets in equities so that you'll have a higher chance of beating inflation every year, and beating it by a higher amount. Also, I still strongly encourage you to stick to the DRREW plan--particularly, always have some amount ready for unexpected expenses and get some form of private health insurance.
Finally, you may want to delay retirement for a few years and maybe build up your funds to 5 or 6 million. Try to play with the equation, change 4 million to a higher amount and instead of 60 change the exponent to years of retirement - 1, and see by how much X will increase.
Labels:
Dear Investor Juan,
Retirement
Thursday, May 23, 2013
The 2013 Philippine Senatorial Elections: A Lesson in Statistics and Framing
I was supposed to finish the draft of my dissertation this afternoon but something more important came up.
This morning, while I was busy watching Game 1 of the Heat-Pacers series (coach Vogel, why did you take Hibbert out in the last couple of plays?) while doing laundry, a wild news article appeared:
Ateneo prof's 60-30-10 poll results pattern gets Comelec's attention
The article talks about Ateneo de Manila Associate Professor Lex Muga and his observation of an "interesting" pattern in the polling of partial results in the last Senatorial elections. And if one takes a look at his recent public Facebook posts on the matter, one will see the following graphics.
While Dr. Muga does not explicitly say anything in his Facebook posts, the article above managed to elicit his more exact thoughts on the matter:
“May pattern. Interesting pattern. Sabi ko nga na parang 60-30-10. Ang tanong ko, bakit ‘pag kunin mo ‘yung mga actual votes sa first canvass, second canvass, kuha sila mula sa isang probinsiya lang bakit 60-30-10 pa rin? Hanggang 16. ‘Di ba manggagaling naman sa iba-ibang probinsiya ang COCs (certificates of canvass) eh? So baka ‘di dapat ganun. Dapat merong variation," Muga said in an interview aired on GMA News' "24 Oras." (Emphasis is mine. - IJ)
In English, "there should be variation in the data," which implies that Dr. Muga sees no variation and that the "60-30-10" pattern is the same across all 16 canvas results.
This is where things turn for the wrong.
One thing that you'll notice in Dr. Muga's statistics and graphics is that there is no mention of sample size, or how large the data set involved is--and inadvertent or not, this is a critical omission. Yes, to the naked eye, the numbers seem to form a pattern. Yes, when our minds look at the data, there don't seem do be any significant differences in the proportion of votes for each coalition from canvas to canvas. However, the problem is that our eyes and minds are not always capable of seeing or comprehending differences that matter. Any student of elementary statistics should know that even seemingly small or immaterial differences matter if the sample is big enough.
All the tools that we need are available to see if there is indeed a statistically significant pattern of constancy in the data. The data that Dr. Muga used is here. And you can follow the results of my analysis with this Excel file.
Some clarifications before we start:
This morning, while I was busy watching Game 1 of the Heat-Pacers series (coach Vogel, why did you take Hibbert out in the last couple of plays?) while doing laundry, a wild news article appeared:
Ateneo prof's 60-30-10 poll results pattern gets Comelec's attention
The article talks about Ateneo de Manila Associate Professor Lex Muga and his observation of an "interesting" pattern in the polling of partial results in the last Senatorial elections. And if one takes a look at his recent public Facebook posts on the matter, one will see the following graphics.
While Dr. Muga does not explicitly say anything in his Facebook posts, the article above managed to elicit his more exact thoughts on the matter:
“May pattern. Interesting pattern. Sabi ko nga na parang 60-30-10. Ang tanong ko, bakit ‘pag kunin mo ‘yung mga actual votes sa first canvass, second canvass, kuha sila mula sa isang probinsiya lang bakit 60-30-10 pa rin? Hanggang 16. ‘Di ba manggagaling naman sa iba-ibang probinsiya ang COCs (certificates of canvass) eh? So baka ‘di dapat ganun. Dapat merong variation," Muga said in an interview aired on GMA News' "24 Oras." (Emphasis is mine. - IJ)
In English, "there should be variation in the data," which implies that Dr. Muga sees no variation and that the "60-30-10" pattern is the same across all 16 canvas results.
This is where things turn for the wrong.
One thing that you'll notice in Dr. Muga's statistics and graphics is that there is no mention of sample size, or how large the data set involved is--and inadvertent or not, this is a critical omission. Yes, to the naked eye, the numbers seem to form a pattern. Yes, when our minds look at the data, there don't seem do be any significant differences in the proportion of votes for each coalition from canvas to canvas. However, the problem is that our eyes and minds are not always capable of seeing or comprehending differences that matter. Any student of elementary statistics should know that even seemingly small or immaterial differences matter if the sample is big enough.
All the tools that we need are available to see if there is indeed a statistically significant pattern of constancy in the data. The data that Dr. Muga used is here. And you can follow the results of my analysis with this Excel file.
Some clarifications before we start:
- What are we trying to prove or disprove? That the pattern that Dr. Muga has observed exists, that the proportion of votes that went to each political coalition is constant from canvas to canvas.
- For the sake of expediency, we will just focus on the proportion of votes for Team PNoy candidates.
- We will use the incremental increases in votes from canvas to canvas. Seriously, it's idiotic to use the cumulative totals: of course it's going to converge to the population average, the denominator keeps on getting bigger and approaching the total number of senator-votes.
- Since each voter can vote for 12 senators, then the appropriate unit of analysis is the senator-vote, where each voter has a maximum of 12 senator-votes. The number of "votes" in the spreadsheet or results are therefore not the same as the number of voters, but rather the number of senator-votes.
Test 1: Comparing confidence intervals
A confidence interval is an interval estimate for a number that we don't know the true value of. For example, if the 95% confidence interval for the proportion of votes that went to Team PNoy is 59% to 61% (or [59%,61%]), then we can say that there is a 95% chance that the true proportion is between 59% and 61%. Why do I use the qualifier "true"? The true proportion is not exactly known because we don't have the complete results yet; each canvas tabulation is just a representative sample of the total population of senator-votes.
In the "PNoy" tab, I have computed for the confidence interval for each sample (i.e., canvas result) using the formula below at the significance levels 0.05 and 0.01 (significance levels basically measure how much room for error you are willing to accept).
Confidence intervals make comparing two estimates easier. Basically, if the confidence intervals for two estimates overlap, then they are statistically equal. BUT if the confidence intervals don't overlap, then there is enough statistical evidence that the estimates are not equal.
In the "PNoy Confidence Intervals" and "PNoy Confidence Intervals (2)" tabs, I have compared the confidence intervals of the proportion estimates for each canvas using significance levels of 0.05 and 0.01, respectively. Both results show that out of 120 confidence interval pairs, only 3 overlap (3 vs. 14, 9 vs. 10, and 6 vs. 8). This means that up to a 1% significance level, 117 out of 120 pairs are statistically different! This method therefore rejects the hypothesis that there is no variation in the data, or that the proportion of votes for Team PNoy is the same from canvas to canvas. Almost all of the proportions are statistically different!
Test 2: Chi-square goodness of fit test
We can use this test for the hypothesis "the proportion of votes that went to each political coalition is constant from canvas to canvas" in one step. The proportion of the total number of votes up to the 16th canvas is 59.63%. If we assume that the same proportion of incremental votes in each canvas voted for Team PNoy, then the coalition should get the expected number of votes E per canvas, as shown in the "Chi Square" tab.
The Chi square statistic is given by
If the statistic is big enough, it means that the set of observed or actual votes (O) for Team PNoy is statistically different from the set of expected votes (E), and the hypothesis is rejected.
The resulting Chi square statistic is 50,000+, which is more than enough to reject the hypothesis. Again, the data shows that the proportion of votes for Team PNoy is statistically different from canvas to canvas.
Test 3: The "Random Coalition" eyeball test
There are plenty of things in statistics (or in the entire universe, actually) that are counter-intuitive or are hard to understand.
Take this last "test," for example. Choose any 9 senatorial candidate at random from the list of 33. I used my calculator's "Ran#" to draft my "dream team" of random senatoriables:
 |
| Please click to enlarge. |
Plotting the percentages using the same axis as Dr. Muga, we get:
What wizardry is this? A similar pattern for a random group of candidates?
We also have to remember, however, that a lot of times, things are not as simple or straightforward as they look. The same data using a different vertical axis:
Replication of graph for Team PNoy proportion of votes that Dr. Muga posted in Facebook:
Same data, using a different vertical axis.
*Sigh*
I'm sure a lot of shenanigans happened in the last elections. There's one more thing that I'm sure of, though: whatever happened is not reflected by the data, and that the "interesting" pattern that Dr. Muga observed does not really exist.
Just remember two things: 1) the sample size matters; and 2) framing matters.
For those who missed it, the Excel file that contains all the data and analysis is here.
Labels:
Does Not Subscribe to Labels
Tuesday, May 21, 2013
An Introduction to the DRREW Framework
DEAR INVESTOR JUAN
Dear Investor Juan,
Hello po and good day!
I have been reading about financial freedom, investing and mutual funds (through Francisco Colayco's book) but it was only until very recently that I put things to heart and thus stumbled upon this blog.
I am 23 years old and just recently gave birth to a healthy baby girl. My partner is 26 years old. I've only really been working full time for a year now and my partner for half so perhaps you can give me some slack and skip on the sermon on why we have not saved much.
We are still on the process of building on our emergency fund and only have around 10k in time deposit. I guess that would pretty much be our net worth (maybe perhaps a little higher if you include the 7k (9k worth, I think) air conditioner plus a few books, some baby stuff and a 1-year-old netbook that we could sell just in case).
Anyway, here is an overview of our monthly expenses:
Utilities/Home Expenses - 10k (we still -shamefully- live with my parents)
Budget for baby - 10k
Daily allowance for me and hubby - 4k
VUL from PRU Life - 3k (I got this for myself before I got pregnant)
Leaving us around 5-6k for savings
Perhaps you could give us advice on what you think of this plan. We used your Budget Planner excel sheet, by the way. We want to build up on our emergency fund but I am also contemplating about investing in mutual funds as well (at least just the initial 5K) since we will be expecting a midyear bonus come June 2013. My plan is to save at least 6K a month, perhaps get the 1k and place it in mutual funds. What do you think?
I know you would not suggest having the VUL but I already got it anyway. My hubby and I are both covered by HMO (plus baby will be soon, as well) and I'm thinking about making the emergency fund as a health fund, for the mean time.
We are also thinking about getting a Volkswagen Beetle which is around 35k-50k - I think it could really help us lessen transportation expenses as we ride the taxi when taking our baby with us. We also have to save up for baby's first birthday February next year (haha) and then eventually for her education, which maybe 50k a year in today's money and rates.
We do have plans of investing in an agricultural lot in the future - in five years, maybe? And then perhaps an apartment in ten. Anything that generates passive income.
Well, my letter is quite long now and it's probably giving you a headache. Compared to your other letter senders, I think we are quite low on money, no? But hey, it's never too late, right? We're still quite young and I also have my parents with me (hehe) whom I can ask for help if really needed. I also keep telling myself that, at least, as early as now, I am already thinking about having financial goals and changing the way we handle our money.
PS. I believe we could really achieve our financial goals - we were able to save up around 50K in just 3 months (and that doesn't count the monthly expenses we had to deal with) in time for my delivery.
PPS. I work as a freelance writer once in a while and I was wondering if you could refer me to the friend you were talking about in one of your blog posts.
Thanks in advance, Investor Juan and more power! And thanks a lot for teaching me so many invaluable lessons in personal finance. :)
Pam
Dear Pam,
First, let me get one thing out of the way: you and your partner are actually doing quite well. You have a positive net worth and presumably not in debt, you're still young, are both employed, and so have plenty of time and opportunities to prepare for the future. And perhaps what's most important is that you are aware of the need to take control of your finances, and have started to do something about it. Believe me, you guys are off to a very good start.
Now let me address your other concerns.
Over the years, I have been developing a framework for managing personal and household finances, an early version of which you may have already come across in this series of posts. The latest version, which I'm presenting for the first time in this post, looks like this:
Stage 1: Eliminate (expensive) Debt
Stage 2: Manage Risk with health and life insurance and an emergency fund
Stage 3: Save and invest for Retirement
Stage 4: Save for discretionary future Expenses
Stage 5: Build-up Wealth
(I hate acronyms, but I guess they're okay if they can help people remember important things... so there you go--DRREW).
I'll explain this framework in a dedicated post in the near future, but for now I think the only item that needs a bit more explaining is "discretionary future expenses." This item consists of high-priced purchases (home or car) and future needs that require a substantial amount of money (wedding, child's future education, European holiday, etc.). Depending on the actual item or need, planning for the purchase or expense may take priority over saving for retirement. For example, you might want to prioritize saving for your child's education over your retirement savings.
So right now, you are in Stage 2. You're employed, so you're amply covered by insurance, and you're starting to build up your emergency fund. Regarding this, I suggest that you take out the 10,000 from the time deposit account and just place it in a savings account. The purpose of an emergency fund is to have money in hand for emergencies so that you won't have to rely on debt (which tends to be expensive if taken on short notice) or selling your assets at a loss. Emergency funds need to be accessible any time, and it's okay if you don't earn interest--remember, you're not saving to get rich, you're saving for emergencies. Since you're spending around 25,000 per month, you have to continue adding to your emergency fund until you accumulate 150,000 to 200,000 pesos.
Regarding the VUL, if it's impossible to get out of the deal without incurring fees or losing more money, then just stay. But please just stick with your premiums and don't invest any more than you have to.
Once you have your emergency fund taken care of, the proceed to Stage 3 and save and invest for retirement. You have determine how much you have to save for this (it's something that I've talked about in the last post and in a future follow-up post). And this is where your plan to invest in property comes in: retirement savings need to be invested in long-term vehicles such as real estate and low-fee equity funds. So you have the right idea, just remember what you are saving for.
I guess that's pretty much all I can offer now. Thanks for the email and congratulations on the great start. I'll email you in private about that writing "racket." Good luck!
Dear Investor Juan,
Hello po and good day!
I have been reading about financial freedom, investing and mutual funds (through Francisco Colayco's book) but it was only until very recently that I put things to heart and thus stumbled upon this blog.
I am 23 years old and just recently gave birth to a healthy baby girl. My partner is 26 years old. I've only really been working full time for a year now and my partner for half so perhaps you can give me some slack and skip on the sermon on why we have not saved much.
We are still on the process of building on our emergency fund and only have around 10k in time deposit. I guess that would pretty much be our net worth (maybe perhaps a little higher if you include the 7k (9k worth, I think) air conditioner plus a few books, some baby stuff and a 1-year-old netbook that we could sell just in case).
Anyway, here is an overview of our monthly expenses:
Utilities/Home Expenses - 10k (we still -shamefully- live with my parents)
Budget for baby - 10k
Daily allowance for me and hubby - 4k
VUL from PRU Life - 3k (I got this for myself before I got pregnant)
Leaving us around 5-6k for savings
Perhaps you could give us advice on what you think of this plan. We used your Budget Planner excel sheet, by the way. We want to build up on our emergency fund but I am also contemplating about investing in mutual funds as well (at least just the initial 5K) since we will be expecting a midyear bonus come June 2013. My plan is to save at least 6K a month, perhaps get the 1k and place it in mutual funds. What do you think?
I know you would not suggest having the VUL but I already got it anyway. My hubby and I are both covered by HMO (plus baby will be soon, as well) and I'm thinking about making the emergency fund as a health fund, for the mean time.
We are also thinking about getting a Volkswagen Beetle which is around 35k-50k - I think it could really help us lessen transportation expenses as we ride the taxi when taking our baby with us. We also have to save up for baby's first birthday February next year (haha) and then eventually for her education, which maybe 50k a year in today's money and rates.
We do have plans of investing in an agricultural lot in the future - in five years, maybe? And then perhaps an apartment in ten. Anything that generates passive income.
Well, my letter is quite long now and it's probably giving you a headache. Compared to your other letter senders, I think we are quite low on money, no? But hey, it's never too late, right? We're still quite young and I also have my parents with me (hehe) whom I can ask for help if really needed. I also keep telling myself that, at least, as early as now, I am already thinking about having financial goals and changing the way we handle our money.
PS. I believe we could really achieve our financial goals - we were able to save up around 50K in just 3 months (and that doesn't count the monthly expenses we had to deal with) in time for my delivery.
PPS. I work as a freelance writer once in a while and I was wondering if you could refer me to the friend you were talking about in one of your blog posts.
Thanks in advance, Investor Juan and more power! And thanks a lot for teaching me so many invaluable lessons in personal finance. :)
Pam
Dear Pam,
First, let me get one thing out of the way: you and your partner are actually doing quite well. You have a positive net worth and presumably not in debt, you're still young, are both employed, and so have plenty of time and opportunities to prepare for the future. And perhaps what's most important is that you are aware of the need to take control of your finances, and have started to do something about it. Believe me, you guys are off to a very good start.
Now let me address your other concerns.
Over the years, I have been developing a framework for managing personal and household finances, an early version of which you may have already come across in this series of posts. The latest version, which I'm presenting for the first time in this post, looks like this:
Stage 1: Eliminate (expensive) Debt
Stage 2: Manage Risk with health and life insurance and an emergency fund
Stage 3: Save and invest for Retirement
Stage 4: Save for discretionary future Expenses
Stage 5: Build-up Wealth
(I hate acronyms, but I guess they're okay if they can help people remember important things... so there you go--DRREW).
I'll explain this framework in a dedicated post in the near future, but for now I think the only item that needs a bit more explaining is "discretionary future expenses." This item consists of high-priced purchases (home or car) and future needs that require a substantial amount of money (wedding, child's future education, European holiday, etc.). Depending on the actual item or need, planning for the purchase or expense may take priority over saving for retirement. For example, you might want to prioritize saving for your child's education over your retirement savings.
So right now, you are in Stage 2. You're employed, so you're amply covered by insurance, and you're starting to build up your emergency fund. Regarding this, I suggest that you take out the 10,000 from the time deposit account and just place it in a savings account. The purpose of an emergency fund is to have money in hand for emergencies so that you won't have to rely on debt (which tends to be expensive if taken on short notice) or selling your assets at a loss. Emergency funds need to be accessible any time, and it's okay if you don't earn interest--remember, you're not saving to get rich, you're saving for emergencies. Since you're spending around 25,000 per month, you have to continue adding to your emergency fund until you accumulate 150,000 to 200,000 pesos.
Regarding the VUL, if it's impossible to get out of the deal without incurring fees or losing more money, then just stay. But please just stick with your premiums and don't invest any more than you have to.
Once you have your emergency fund taken care of, the proceed to Stage 3 and save and invest for retirement. You have determine how much you have to save for this (it's something that I've talked about in the last post and in a future follow-up post). And this is where your plan to invest in property comes in: retirement savings need to be invested in long-term vehicles such as real estate and low-fee equity funds. So you have the right idea, just remember what you are saving for.
I guess that's pretty much all I can offer now. Thanks for the email and congratulations on the great start. I'll email you in private about that writing "racket." Good luck!
Friday, May 17, 2013
The 30-60-90 Approach to Retirement Planning, Part 1: Estimating Monthly Expenses
This is something that I have been working on in the past couple of months, and I feel that now is a good time to share it with you.
The right way to do retirement or financial planning is to estimate future annual earnings and expenses, before and after retirement, using a set of assumptions as I have demonstrated here and here. The problem with this approach is that it may be too complex and daunting for many individuals. The 30-60-90 framework is a simple, easy to use and understand tool for estimating the amount one needs to save in order to cover retirement expenses. Despite its simplicity, the approach is well grounded in theory as it considers important considerations such as inflation and investment returns.
30-60-90?
The name comes from the premise that an individual would start to save for retirement at 30, retire at 60, and pass away at 90; the implication that the saving period equals the retirement (or zero income) period equals 30 years makes a simpler analysis possible. Being in a 30-60-90 situation means that you have 30 years to earn what you expect or aim to spend in your 30 years of retirement. Ignoring inflation and interest for the moment, this means that by the time you retire you will have accumulated 3 million pesos in wealth, which you will then use in equal increments of 100,000 per year in the next 30 years and your wealth will have been depleted to zero at the end of your 90th year. (While the 30-60-90 scenario may not perfectly fit everyone, it's a good enough description of a person's condition such that whatever accuracy is lost is made up for by the usefulness of the model. In any case, the model is easy enough to adjust to a comparable configuration such as 35-60-85 or 40-60-80, as long as the saving period is the same as the retirement period and you're comfortable with the life expectancy estimate).
The question is, in a 30-60-90 scenario, how much do you actually have to save per month or per year for retirement, given your chosen lifestyle, inflation, and the possibility of earning from investments? To find an answer, let's take look at the situation in another way. The image above shows how your total wealth will behave given the saving and spending pattern described previously. What we can do is rearrange some of the green "blocks" above and invert the right side of the pyramid so that it will look like this:
In the first image, it seems that the first 100,000 deposit takes 59 years before it is used up, the second 100,000 takes 57 years, and so on, until the 29th 100,000 lasts for three years, and the final 100,000 (the tip of the pyramid) gets used up in one year (the 60th year). If we rearrange the blocks like in the second image, instead of having multiple/different horizons for your deposits, now each 100,000 deposit gets withdrawn after 30 years, and all deposits have the same 30-year horizon.
This is what makes the 30-60-90 tool useful: it assumes that whatever you set aside for retirement in a particular month or year, you withdraw and use 30 years later. And since all deposits to your retirement fund have the same horizon, you just have to compute for one amount that you need to save in a particular month or year.
Estimating retirement expenses
The process starts by estimating your monthly or annual expenses for when you retire but at today's prices. If you want to maintain your current lifestyle, just estimate your personal expenses per month, on average; adjust the amount upward or downward if you prefer a more comfortable or a simpler lifestyle, respectively. Do not adjust for inflation--at least not yet, we'll go to that later. Also, estimate only your personal retirement expenses--not your wife's or whoever else's--unless your wife is a home-maker (i.e., unemployed for life) and do not include discretionary expenses such as your child's college tuition as these will have to be considered separately. The basic components of your estimate should be food, rent/housing, and transportation.
To give you an example, I recently asked a good friend to do this exercise. According to him, he would need 400 pesos per day for food and other daily expenses, and 20,000 per month for rent and car payments, which amounts to 32,000 pesos per month in today's peso.
If we live in a world where prices are constant and investments don't earn returns, using the 30-60-90 framework, my friend has to save 32,000 per month just to meet his retirement expenses given his chosen lifestyle. Seems daunting, doesn't it? What if we consider inflation, and my friend just chooses to tuck away his savings in a bank savings account? Then he'll definitely need to save more than 32,000 per month today. How about if he invests his retirement fund in a "riskier" investment such as an equity UITF, how will this affect his savings goal?
In Part 2 next week, we'll discuss exactly how inflation and investment returns figure into the model. For now, try to estimate your monthly retirement expense in today's peso and see if you can afford to save that amount.
Have a great weekend!
The right way to do retirement or financial planning is to estimate future annual earnings and expenses, before and after retirement, using a set of assumptions as I have demonstrated here and here. The problem with this approach is that it may be too complex and daunting for many individuals. The 30-60-90 framework is a simple, easy to use and understand tool for estimating the amount one needs to save in order to cover retirement expenses. Despite its simplicity, the approach is well grounded in theory as it considers important considerations such as inflation and investment returns.
30-60-90?
The name comes from the premise that an individual would start to save for retirement at 30, retire at 60, and pass away at 90; the implication that the saving period equals the retirement (or zero income) period equals 30 years makes a simpler analysis possible. Being in a 30-60-90 situation means that you have 30 years to earn what you expect or aim to spend in your 30 years of retirement. Ignoring inflation and interest for the moment, this means that by the time you retire you will have accumulated 3 million pesos in wealth, which you will then use in equal increments of 100,000 per year in the next 30 years and your wealth will have been depleted to zero at the end of your 90th year. (While the 30-60-90 scenario may not perfectly fit everyone, it's a good enough description of a person's condition such that whatever accuracy is lost is made up for by the usefulness of the model. In any case, the model is easy enough to adjust to a comparable configuration such as 35-60-85 or 40-60-80, as long as the saving period is the same as the retirement period and you're comfortable with the life expectancy estimate).
 |
| Click to enlarge |
 |
| Click to enlarge |
This is what makes the 30-60-90 tool useful: it assumes that whatever you set aside for retirement in a particular month or year, you withdraw and use 30 years later. And since all deposits to your retirement fund have the same horizon, you just have to compute for one amount that you need to save in a particular month or year.
Estimating retirement expenses
The process starts by estimating your monthly or annual expenses for when you retire but at today's prices. If you want to maintain your current lifestyle, just estimate your personal expenses per month, on average; adjust the amount upward or downward if you prefer a more comfortable or a simpler lifestyle, respectively. Do not adjust for inflation--at least not yet, we'll go to that later. Also, estimate only your personal retirement expenses--not your wife's or whoever else's--unless your wife is a home-maker (i.e., unemployed for life) and do not include discretionary expenses such as your child's college tuition as these will have to be considered separately. The basic components of your estimate should be food, rent/housing, and transportation.
To give you an example, I recently asked a good friend to do this exercise. According to him, he would need 400 pesos per day for food and other daily expenses, and 20,000 per month for rent and car payments, which amounts to 32,000 pesos per month in today's peso.
If we live in a world where prices are constant and investments don't earn returns, using the 30-60-90 framework, my friend has to save 32,000 per month just to meet his retirement expenses given his chosen lifestyle. Seems daunting, doesn't it? What if we consider inflation, and my friend just chooses to tuck away his savings in a bank savings account? Then he'll definitely need to save more than 32,000 per month today. How about if he invests his retirement fund in a "riskier" investment such as an equity UITF, how will this affect his savings goal?
In Part 2 next week, we'll discuss exactly how inflation and investment returns figure into the model. For now, try to estimate your monthly retirement expense in today's peso and see if you can afford to save that amount.
Have a great weekend!
Labels:
Retirement
Wednesday, May 15, 2013
Invitation for the First Philippine Junior Finance and Investment Summit
DEAR INVESTOR JUAN
This request is from one of my former students. Since CFA Philippines is a non-profit entity, I feel that promoting one of their events on the blog does not violate my self-imposed ban on advertising.
***
Dear Investor Juan,
Good day!
The Chartered Financial Analyst Society of the Philippines (“CFA Philippines”), a non-profit professional membership organization of finance and investment practitioners will be holding its “First Philippine Junior Finance and Investment Summit” on July 6, 2013, Saturday, from 9:00 A.M. to 5:00 P.M at the SMX Convention Centre. This event aims to enhance financial literacy and elevate the quality of the finance profession in the country. This finance career and educational campaign will help students and young professionals prepare for a career in the finance and investment industry through presentations and discussion forums.
So far, we have invited well-known and seasoned speakers to talk in this event. I believe the admission fee will be less than Php 500 including packed lunch and snacks (emphasis is mine - IJ). Hope you can help us promote the event! :D
Confirmed speakers are:
Philippine Economy: Asian Perspective
International Monetary Fund
Peiris, Shanaka Jayanath
Stock Market Investments
COL Financial Group
April Lynn Tan, CFA
Trust Products
Banco de Oro Unibank
Marvin Fausto
Discussion on Careers in Finance and Investment Industry
Ayala Corporation
Ginaflor Oris, CFA
Bangko Sentral ng Pilipinas
Mary Jane Chiong, CFA
HSBC
Maria Corazon Dela Cruz-Purisima
(There are some other important speakers who have been invited, but I have removed their names from the list since their attendance has not yet been confirmed. -IJ)
Regards,
Jane
***
The registration procedure is still in the works, so until it is finalized feel free to visit the event's Facebook page for updates.
This request is from one of my former students. Since CFA Philippines is a non-profit entity, I feel that promoting one of their events on the blog does not violate my self-imposed ban on advertising.
***
Dear Investor Juan,
Good day!
The Chartered Financial Analyst Society of the Philippines (“CFA Philippines”), a non-profit professional membership organization of finance and investment practitioners will be holding its “First Philippine Junior Finance and Investment Summit” on July 6, 2013, Saturday, from 9:00 A.M. to 5:00 P.M at the SMX Convention Centre. This event aims to enhance financial literacy and elevate the quality of the finance profession in the country. This finance career and educational campaign will help students and young professionals prepare for a career in the finance and investment industry through presentations and discussion forums.
So far, we have invited well-known and seasoned speakers to talk in this event. I believe the admission fee will be less than Php 500 including packed lunch and snacks (emphasis is mine - IJ). Hope you can help us promote the event! :D
Confirmed speakers are:
Philippine Economy: Asian Perspective
International Monetary Fund
Peiris, Shanaka Jayanath
Stock Market Investments
COL Financial Group
April Lynn Tan, CFA
Trust Products
Banco de Oro Unibank
Marvin Fausto
Discussion on Careers in Finance and Investment Industry
Ayala Corporation
Ginaflor Oris, CFA
Bangko Sentral ng Pilipinas
Mary Jane Chiong, CFA
HSBC
Maria Corazon Dela Cruz-Purisima
(There are some other important speakers who have been invited, but I have removed their names from the list since their attendance has not yet been confirmed. -IJ)
Regards,
Jane
***
The registration procedure is still in the works, so until it is finalized feel free to visit the event's Facebook page for updates.
Labels:
Dear Investor Juan
Friday, May 10, 2013
Frontline: Secret History of the Credit Card
Here's another "must watch" from Frontline on PBS. "Things I Learned..." next week. Have a great weekend, everybody!
Chapter 1
Chapter 2
Chapter 3
Chapter 4
Chapter 5
Labels:
Credit Cards,
Videos
Tuesday, May 7, 2013
Housing Loan Lump Sum Payments
DEAR INVESTOR JUAN
Dear Investor Juan,
I hope everything is well with you.
Are you familiar with loan amortization? My wife and I have a housing loan with a term of 20 years. Our goal is to shortened that to at most 15 years. We have discussed this with our bank and they said that they don’t usually reconstruct loan. We can try but it has a high probability that we will not be approved. So they suggested to us to pay in lump sum every annual repricing. There is no minimum amount for the lump sum payment but their suggestion is it has to be at least 6 times of our monthly amortization if possible so that it can also somehow lower our amortization. It will probably take us 2-3 years to save that amount of money (around 100k). Is it wise to do that or paying in lump sum every year even if it is only 30-50k a wiser move?
We got a fixed interest rate for the first 3 years. I can easily compute the amortization in Excel via the Loan Amortization template. I don’t know what will be the computation for the repricing in the 4th year and onwards that is way I can’t come up which is better. J
Here is the sample data that I used in computing for the amortization for Year 1 to 3 using Excel.
Loan Amount: 2,000,000
Annual interest rate: 7.88%
Loan period in years: 20
Number of payments per year: 12
Is this the correct computation for year 4?
Loan Amount: 1,860,550.26
Annual interest rate: 8%
Loan period in years: 17 ???
Number of payments per year: 12
Thank you so much.
Danison
Dear Danison,
So your objective is to shorten the term of your housing loan from 20 to 15 years by either paying a lump sum of 100,000 on the fourth year or annual payments of 30,000 to 50,000.
Using the information you have provided me, I have reconstructed your loan amortization schedule here. You have a 20-year loan with an annual interest rate of 7.88% (we'll get back to this later). Using the PMT function of Google Spreadsheet (same as in Excel; "Current" worksheet, double-click cell B4 to see the inputs), we can compute for the monthly amortization of your loan: 16,580 pesos per month. If you paid down payment on your loan, you should actually deduct it from the loan amount, and it will give you a lower amortization. Also, the resulting amount does not include insurance and other fees, so it may differ a bit from what your bank quoted.
The monthly amortization amount is what you have to pay every month to pay off your loan. Every month, a portion of it is used to pay for the interest of your loan, and the remainder goes to the repayment of principal (see the formulas for the cells in the "Interest payment" and "Principal payment" columns. So every month, a portion of the principal is repaid, the loan balance gets smaller, the interest payment correspondingly decreases, and a bigger portion of the amortization goes to principal. In the "Current" worksheet, you'll see how much of the amortization goes to interest, how much goes to principal, and what the loan balance is every month. At the end of 20 years or 240 months, you'll see that the ending balance is zero and the loan will have been completely paid off.
Now go to the "Lump Sum" worksheet to see how much impact a 100,000 peso payment will make. If you make a lump sum payment, the entire amount will go to principal and this will accelerate the repayment of the loan. To see how it will affect the schedule, just manually add the amount to the "Principal payment" cell for the month of your choice. Here, I assumed that you will make the payment at the end of Year 3.
If you go to the bottom of the worksheet, you'll see that with this lump sum payment you will be able to completely pay off the loan at the end of Month 219, or near the beginning of Year 19. So it seems that you would have to make more lump sum payments if you want to completely pay off the loan by Year 15 (Month 180). Feel free to play with the spreadsheet and add whatever lump sum amounts you think you can afford to achieve your goal.
In another email, you mentioned that the interest rate of your loan will be readjusted for Year 4 onward. In the "Adjusted Rate" worksheet, you'll see how a different rate will affect your subsequent payments. You're currently in Year 3, so with the recent credit rating upgrades, you should expect a lower readjusted rate next year (I assumed 6%).
Anyway, I know that I did not really answer your questions, sorry about that, but rather gave you a tool that can hopefully help you find the answers yourself. Good luck!
In case anyone missed it, you'll find the spreadsheet here.
Dear Investor Juan,
I hope everything is well with you.
Are you familiar with loan amortization? My wife and I have a housing loan with a term of 20 years. Our goal is to shortened that to at most 15 years. We have discussed this with our bank and they said that they don’t usually reconstruct loan. We can try but it has a high probability that we will not be approved. So they suggested to us to pay in lump sum every annual repricing. There is no minimum amount for the lump sum payment but their suggestion is it has to be at least 6 times of our monthly amortization if possible so that it can also somehow lower our amortization. It will probably take us 2-3 years to save that amount of money (around 100k). Is it wise to do that or paying in lump sum every year even if it is only 30-50k a wiser move?
We got a fixed interest rate for the first 3 years. I can easily compute the amortization in Excel via the Loan Amortization template. I don’t know what will be the computation for the repricing in the 4th year and onwards that is way I can’t come up which is better. J
Here is the sample data that I used in computing for the amortization for Year 1 to 3 using Excel.
Loan Amount: 2,000,000
Annual interest rate: 7.88%
Loan period in years: 20
Number of payments per year: 12
Is this the correct computation for year 4?
Loan Amount: 1,860,550.26
Annual interest rate: 8%
Loan period in years: 17 ???
Number of payments per year: 12
Thank you so much.
Danison
Dear Danison,
So your objective is to shorten the term of your housing loan from 20 to 15 years by either paying a lump sum of 100,000 on the fourth year or annual payments of 30,000 to 50,000.
Using the information you have provided me, I have reconstructed your loan amortization schedule here. You have a 20-year loan with an annual interest rate of 7.88% (we'll get back to this later). Using the PMT function of Google Spreadsheet (same as in Excel; "Current" worksheet, double-click cell B4 to see the inputs), we can compute for the monthly amortization of your loan: 16,580 pesos per month. If you paid down payment on your loan, you should actually deduct it from the loan amount, and it will give you a lower amortization. Also, the resulting amount does not include insurance and other fees, so it may differ a bit from what your bank quoted.
The monthly amortization amount is what you have to pay every month to pay off your loan. Every month, a portion of it is used to pay for the interest of your loan, and the remainder goes to the repayment of principal (see the formulas for the cells in the "Interest payment" and "Principal payment" columns. So every month, a portion of the principal is repaid, the loan balance gets smaller, the interest payment correspondingly decreases, and a bigger portion of the amortization goes to principal. In the "Current" worksheet, you'll see how much of the amortization goes to interest, how much goes to principal, and what the loan balance is every month. At the end of 20 years or 240 months, you'll see that the ending balance is zero and the loan will have been completely paid off.
Now go to the "Lump Sum" worksheet to see how much impact a 100,000 peso payment will make. If you make a lump sum payment, the entire amount will go to principal and this will accelerate the repayment of the loan. To see how it will affect the schedule, just manually add the amount to the "Principal payment" cell for the month of your choice. Here, I assumed that you will make the payment at the end of Year 3.
If you go to the bottom of the worksheet, you'll see that with this lump sum payment you will be able to completely pay off the loan at the end of Month 219, or near the beginning of Year 19. So it seems that you would have to make more lump sum payments if you want to completely pay off the loan by Year 15 (Month 180). Feel free to play with the spreadsheet and add whatever lump sum amounts you think you can afford to achieve your goal.
In another email, you mentioned that the interest rate of your loan will be readjusted for Year 4 onward. In the "Adjusted Rate" worksheet, you'll see how a different rate will affect your subsequent payments. You're currently in Year 3, so with the recent credit rating upgrades, you should expect a lower readjusted rate next year (I assumed 6%).
Anyway, I know that I did not really answer your questions, sorry about that, but rather gave you a tool that can hopefully help you find the answers yourself. Good luck!
In case anyone missed it, you'll find the spreadsheet here.
Labels:
Dear Investor Juan,
Debt
Friday, May 3, 2013
12 Things That I've Learned from "The Retirement Gamble"
If you have not seen "The Retirement Gamble" yet, what better time than now? If you think it's not worth spending 60 minutes of your time or the topic is irrelevant to you, maybe my notes can change your mind.
1. According to Robert Hiltonsmith, the economist who first exposed the 401(k) fee "scandal" in the US, one needs to save around 10 to 15% of earnings for retirement, which is way lower that my estimate (40% on a 30,000 pesos per month income) in an earlier post. Obviously, the appropriate savings rate is a function of income: the less you earn, the more you need to save. Think about that statement for a minute and you'll see how ironically and sadly true it is.
2. It's hard to think of retirement since it's so far off into the future, said the lady professor in an interview. If you've just started thinking about retirement now, then you know how true this statement is. It also shows that a big part of the retirement planning "problem" is psychological.
3. The later you start, the harder it gets. The later you start, the more you have to save (as a proportion of your earnings). Start late enough, and you'll find yourself needing to work just to survive. No more retirement, just lifetime employment.
4. Not planning properly (or at all) may force you to use your retirement savings for other things like the education of your children, and this is something that you should avoid doing. Plan carefully and prepare for (i.e., save for) both retirement and discretionary expenses.
5. Three things that you have to think about when planning for retirement: how much to save; how to invest; and how to withdraw money.
6. In a bull run, you can't lose money in the market, even if you're stupid. Which is exactly what's happening now: everyone thinks he or she is an investment genius. The question is where does the bull end and the bear begin?
7. Investment risks are real. There's this one guy whose 13 years worth of returns was wiped out in a blink of an eye.
8. Fees matter. Costs are compounded over time the same way returns are. If you don't want to believe me, believe Jack Bogle (I wish I'll be as lucid and sharp as he is when I turn 83!).
9. There is ample academic evidence that investment/mutual funds can't beat the market systematically and consistently over long horizons. So why pay a premium for fund management if it's highly likely that a lower-costing fund can provide the same returns? Choose low-fee funds such as index funds. In the Philippines, index funds aren't the cheapest, which is a blatant scam. Reminds me of my favorite Dilbert strip:
10. The mutual fund industry is rigged against human psychology. People believe that funds that do well in the past will continue to do well in the future, fine print notwithstanding.
11. Even fund managers own index funds, they just don't talk about it.
12. Get advice from an adviser, not from a salesperson. The person who is selling you investment/mutual funds is a salesperson. And no one sells anything on this blog.
1. According to Robert Hiltonsmith, the economist who first exposed the 401(k) fee "scandal" in the US, one needs to save around 10 to 15% of earnings for retirement, which is way lower that my estimate (40% on a 30,000 pesos per month income) in an earlier post. Obviously, the appropriate savings rate is a function of income: the less you earn, the more you need to save. Think about that statement for a minute and you'll see how ironically and sadly true it is.
2. It's hard to think of retirement since it's so far off into the future, said the lady professor in an interview. If you've just started thinking about retirement now, then you know how true this statement is. It also shows that a big part of the retirement planning "problem" is psychological.
3. The later you start, the harder it gets. The later you start, the more you have to save (as a proportion of your earnings). Start late enough, and you'll find yourself needing to work just to survive. No more retirement, just lifetime employment.
4. Not planning properly (or at all) may force you to use your retirement savings for other things like the education of your children, and this is something that you should avoid doing. Plan carefully and prepare for (i.e., save for) both retirement and discretionary expenses.
5. Three things that you have to think about when planning for retirement: how much to save; how to invest; and how to withdraw money.
6. In a bull run, you can't lose money in the market, even if you're stupid. Which is exactly what's happening now: everyone thinks he or she is an investment genius. The question is where does the bull end and the bear begin?
7. Investment risks are real. There's this one guy whose 13 years worth of returns was wiped out in a blink of an eye.
8. Fees matter. Costs are compounded over time the same way returns are. If you don't want to believe me, believe Jack Bogle (I wish I'll be as lucid and sharp as he is when I turn 83!).
9. There is ample academic evidence that investment/mutual funds can't beat the market systematically and consistently over long horizons. So why pay a premium for fund management if it's highly likely that a lower-costing fund can provide the same returns? Choose low-fee funds such as index funds. In the Philippines, index funds aren't the cheapest, which is a blatant scam. Reminds me of my favorite Dilbert strip:
10. The mutual fund industry is rigged against human psychology. People believe that funds that do well in the past will continue to do well in the future, fine print notwithstanding.
11. Even fund managers own index funds, they just don't talk about it.
12. Get advice from an adviser, not from a salesperson. The person who is selling you investment/mutual funds is a salesperson. And no one sells anything on this blog.
Labels:
Financial Planning,
Lists,
Retirement
Subscribe to:
Posts (Atom)




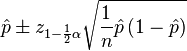







.png)

